密码学期末复习

密码

类别	子类别	算法名称	标准类型	核心参数	基本结构 / 原理
对称密码	分组密码	DES	国际标准	分组: 64-bit, 密钥: 56-bit	16轮 Feistel
		3DES	国际标准	密钥: 112-bit 或 168-bit	EDE (加密-解密-加密)
		AES	国际标准	分组: 128-bit, 密钥: 128/192/256-bit	10/12/14轮 SPN
		SM4	中国标准	分组: 128-bit, 密钥: 128-bit	32轮非平衡Feistel
		IDEA	国际标准	分组: 64-bit, 密钥: 128-bit	混合不同代数群的运算（异或、模加、模乘）
	流密码	RC4	曾广泛使用	密钥长度可变，核心为256字节的S盒	基于非线性数组变换
		ZUC	中国标准	128位密钥和128位初始向量	线性反馈移位寄存器（LFSR）和非线性函数组合
非对称密码	公钥加密/数字签名	RSA	国际标准	密钥长度: 1024-2048-bit	安全性基于大整数分解难题
		ElGamal	国际标准	密文长度是明文2倍	安全性基于离散对数问题 (DLP)
		ECC (椭圆曲线)	国际标准	密钥长度短（如160-bit）	安全性基于椭圆曲线上的离散对数问题 (ECDLP)
		SM2	中国标准	-	基于椭圆曲线密码
	密钥交换	Diffie-Hellman	国际标准	-	安全性基于离散对数问题 (DLP)
Hash函数	-	MD5	曾广泛使用	输出: 128-bit	MD迭代结构
	-	SHA-1	国际标准	输出: 160-bit	MD迭代结构
	-	SHA-2 (SHA-256/512)	国际标准	输出: 256/512-bit	MD迭代结构
	-	SHA-3 (Keccak)	国际标准	可变长度输出	海绵 (Sponge) 结构
	-	SM3	中国标准	输出: 256-bit	MD迭代结构

---

一、绪论

安全属性（目标）

CIA三要素：机密性、完整性、认证性
五大基本目标

• 机密性：信息不泄露给非授权实体
• 完整性：未经授权不能篡改信息
• 可用性：保障资源随时可提供服务
• 认证性：实体本身被正确标识
• 不可抵赖性：用户不能在事后否认信息的生成行为

攻击

被动攻击：指攻击者窃听和分析通信内容，不改变信息

• 主要威胁机密性

主动攻击：指攻击者对数据流进行篡改、伪造或中断

• 主要威胁完整性、认证性、可用性

密码学发展史

两次飞跃

• 科学化：1949年，香农（Shannon）发表 《保密系统的通信理论》
• 公钥密码：1976年，Diffie和Hellman在 《密码学的新方向》 提出了公钥密码体制

重要里程碑

• DES：第一个被广泛应用于商用领域的公开加密算法
• RSA：第一个成熟且应用广泛的公钥密码算法

攻击类型

• 唯密文攻击：攻击者仅拥有截获的密文
• 已知明文攻击：攻击者拥有一组或多组“明文-密文”对
• 选择明文攻击：攻击者可以选择任意明文，并获取其对应的密文
• 选择密文攻击：攻击者可以选择任意密文，并获取其对应的明文

柯克霍夫原则

密码系统的安全性不应依赖于对算法本身的保密，而应仅仅依赖于对密钥的保密
假设：密码分析者已有密码算法及其实现的全部资料。

密码体制分类

根据密钥分

• 对称密码（单钥、私钥）：加密密钥和解密密钥相同，或可以相互推导
• 非对称密码（公钥）：加密密钥（公钥）和解密密钥（私钥）不同，且不能相互推导

按明文处理方式分 (通常指对称密码)

• 流密码：逐比特或逐字节处理明文
• 分组密码：将明文分成固定大小的块进行处理

---

二、古典密码学

代换密码

将明文字母替换成其他字母、数字或符号

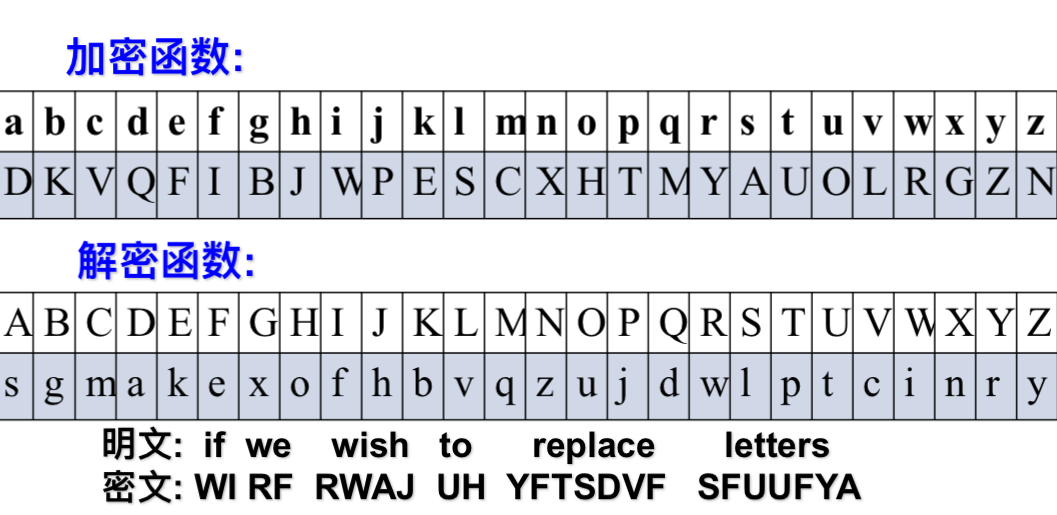
单表代换密码

移位密码 （凯撒密码）

密钥是代换表
破解：穷举搜索，复杂度25；统计攻击

令k=3
明文：meet me after the toga party
密文：PHHW PH DIWHU WKH WRJD SDUWB

仿射密码

• 穷举搜索复杂度$\Phi(26)*26$
• 统计攻击，复杂度$26^2$

密钥$k=(7,3)$，且$gcd(7,26)=1$，明文$hot=(7,14,19)$

• 加密：
  $(7 × 7+3)\mod 26=0$
  $(7 × 14+3)\mod 26=23$
  $(7 × 19+3)\mod 26=6$
  密文为$(0,23,6)=(a,x,g)$
• 解密：对密钥7求逆元 $7^{-1}=15 \mod26$
  解密是加密的逆过程
  $(0-3)×15\mod 26=7$
  $(23-3)×15\mod 26=14$
  $(6-3)×15\mod 26=19$
  明文为$(7,14,19)=(h,o,t)$

单表代换

• 穷举搜索复杂度$26!$，不可行
• 统计攻击可以

多表代换（维吉尼亚密码）

唯密文攻击

单表代换

多表代换

确定密钥长度

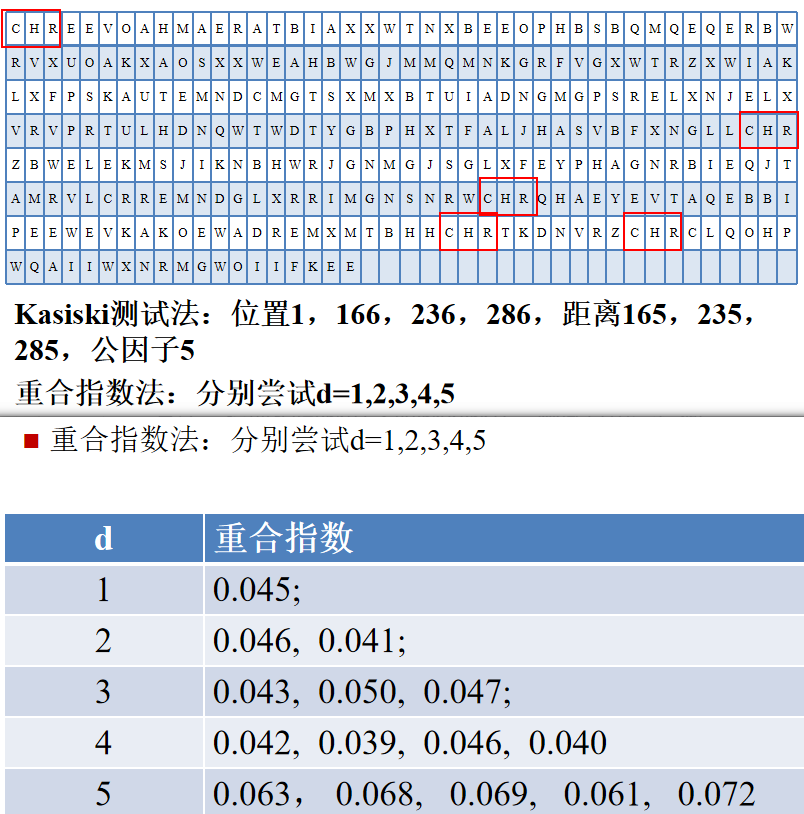
Kasiski测试法

将密文中相同的字母找出来，找出相同字母数的最大公因子

重合指数法

完全随机文本CI=0.0385
有信息冗余的英文文本CI=0.065
$CI=\frac{∑f_i​(f_i​−1)}{n(n-1)}$

确定密钥字相对位移

拟重合指数法-Chi测试

唯密文攻击的作用

• 区分单表代换密码（CI接近0.065）和多表代换密码（CI接近0.0385）
• 确定两段文本是否使用同一种方法进行加密
  • 同一加密方法重合指数CI相近

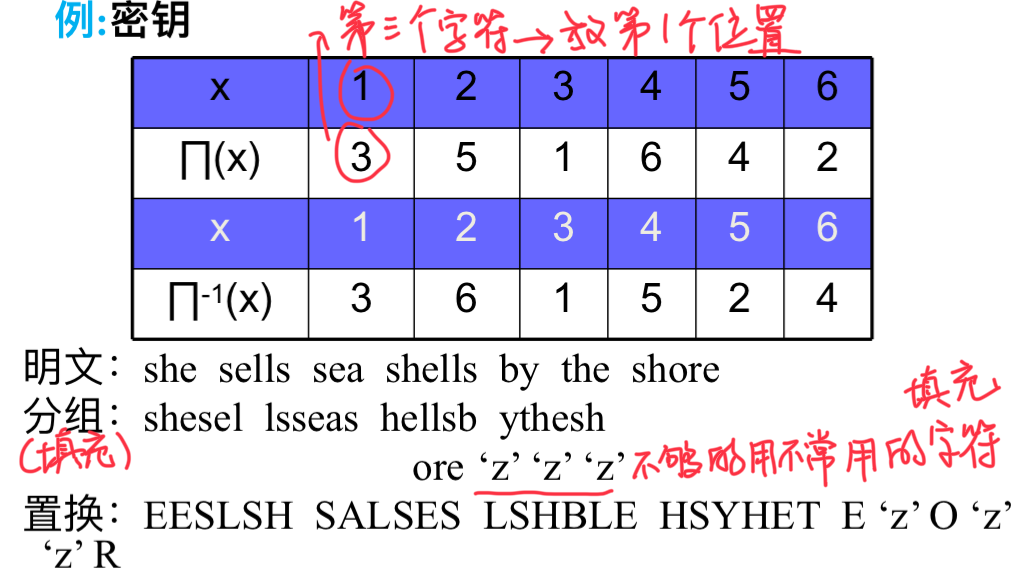
置换密码

不改变明文字母，而是将它们的位置重新排列

Hill（希尔）密码

希尔密码实现了扩散 (Diffusion) 的思想

• 容易被已知明文攻击破解

---

三、密码学基础

香农理论与无条件安全

Shannon通信保密系统

密码体制是一个五元组：$(P,C,K,E,D)$

• $P$—明文空间
• $C$—密文空间
• $K$—密钥空间
• $E$—加密交换
• $D$—解密变换

熵

度量不确定性 ：熵越大，不确定性越高
$H(X) = -\sum_{i} p(x_i) \log_{2} p(x_i)$
当所有事件等概率 发生时，熵取到最大值
$X$为确定事件→$H(X)=0$
$X$均匀分布→$H(X)=\log_{2} n$

$X$表示输入空间，$Y$表示输出空间

• 含糊度：$H(X|Y)$
• 散布度：$H(Y|X)$

$X$熵的减少量：$I(X,Y)=H(X)-H(X|Y)$

完全保密性（无条件安全）

定义：一个密码系统是“完全保密”的，如果密文没有泄露任何关于明文的信息
充分必要条件：$H(P|C)=H(P) 或 I(P,C)=0$
实现的条件：密钥的不确定性必须大于或等于 明文的不确定性
唯一实例：一次一密

复杂度理论与计算安全

算法复杂度

时间（计算）复杂性
空间复杂性
数据复杂性

问题复杂性

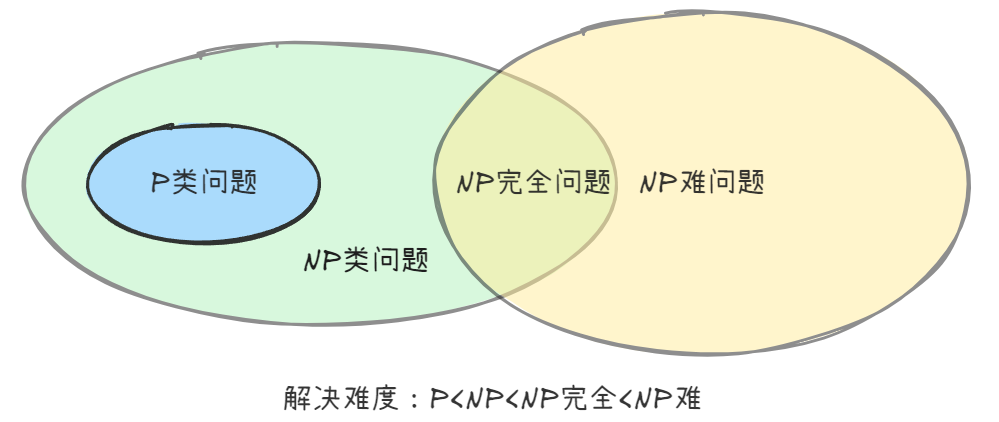
P问题：一个判定问题存在解 的多项式时间算法
NP问题：一个判定问题不存在解 的多项式时间算法；对于一个解答可以在多项式时间验证 其是否正确
NPC（NP完全问题）：NP中任何一个问题都可多项式时间转化为该NP问题，则该NP问题为NP完全问题
NP难问题：为解决NP问题A，将A约化为问题B，解决B的同时也间接解决了问题A，则B为NP难问题

计算安全性

实际安全

• 破解该密码系统的成本超过被加密信息本身价值
• 破译该密码系统的时间超过被加密信息的有效生命周期

---

四、分组密码

分组密码设计的基本技术包含（混乱 ）（扩散 ）和（迭代结构 ）

两大设计原则

扩散：让明文或密钥的单个比特的变化尽可能大地影响到密文的多个比特

• DES：P盒置换
• AES：行移位 和列混合

混乱：使密钥和密文之间的关系尽可能地复杂，让攻击者无法通过分析密文来推断密钥

• DES：S盒
• AES：字节代换

两大迭代结构

• Feistel网络：将数据块分成左右两半，每轮只对其中一半进行加密，然后与另一半异或，再交换两半
  • 加密解密运算过程一样
• SPN网络：通过交替使用代换 (S盒) 和置换 (P盒) 进行多轮迭代

DES算法（数据加密标准）

• 分组长度：64比特
• 密钥长度：56比特（输入为64比特，其中8位为奇偶校验位）

整体结构

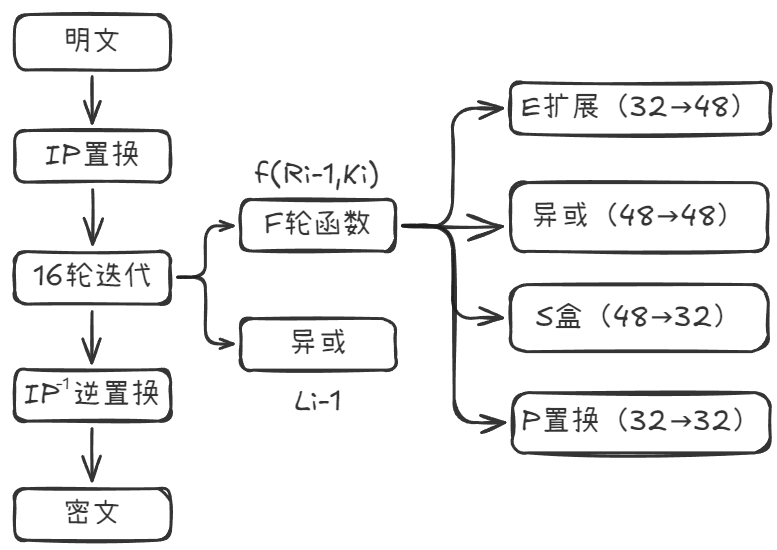
• 初始置换$IP$：$P_0=IP(P)=L_0R_0$
• 16轮迭代：
  • $L_i=R_{i-1}$
  • $R_i=L_{i-1}\oplus f(R_{i-1},K_i)$
• 逆置换$IP^{-1}$：对比特串 $R_{16}L_{16}$ 使用逆置换得到密文 $C$，即 $C={IP}^{-1}(R_{16}L_{16})$

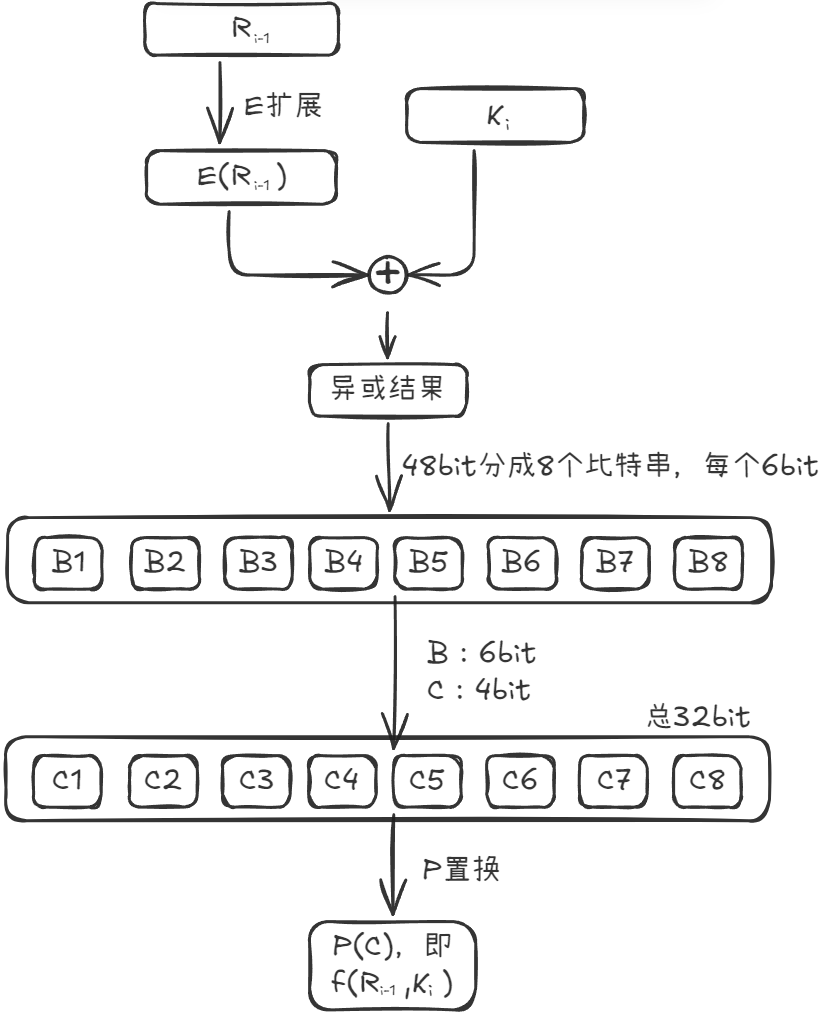
轮函数

• E扩展
• 密钥加
• S盒代换
• P置换
  

密钥编排

从56比特的主密钥生成16个48比特的轮密钥

• 初始$PC1$置换
• 循环左移
• $PC2$置换

解密流程

• 初始置换$IP$
• 轮函数：进行16轮迭代，每轮包括E扩展、S盒替换和P置换，但轮密钥的使用顺序与加密过程相反
• 逆初始置换$IP^{-1}$：对16轮迭代后的数据进行逆初始置换，得到64位明文

DES安全性

弱密钥（有4个）：对所有 $x$ ，都有 $E_K(E_K(x))=x$
半弱密钥（有12个）：密钥对 $(K,K^{'})$ ，满足$E_K(E_{K^{'}})=x$

Triple-DES（其中一种）

$3E((k_1,k_2,k_3),m)=E(k_3,E(k_2,E(k_1,m)))$ 密钥长度=3×56=168bits
穷举攻击复杂度 $2^{168}$ ，中间相遇攻击复杂度 $2^{112}$

中间相遇攻击

双重DES是不安全的，因为中间相遇攻击使复杂度降至$O(2^{56})$，攻击方法与上面的类似

AES算法（高级加密标准）

• 分组长度：128bit
• 密钥长度：128/192/256bit
• 轮数：10/12/14
• 以字节为单位进行处理，将128比特的输入数据看作一个4x4的字节矩阵，称为状态

整体结构

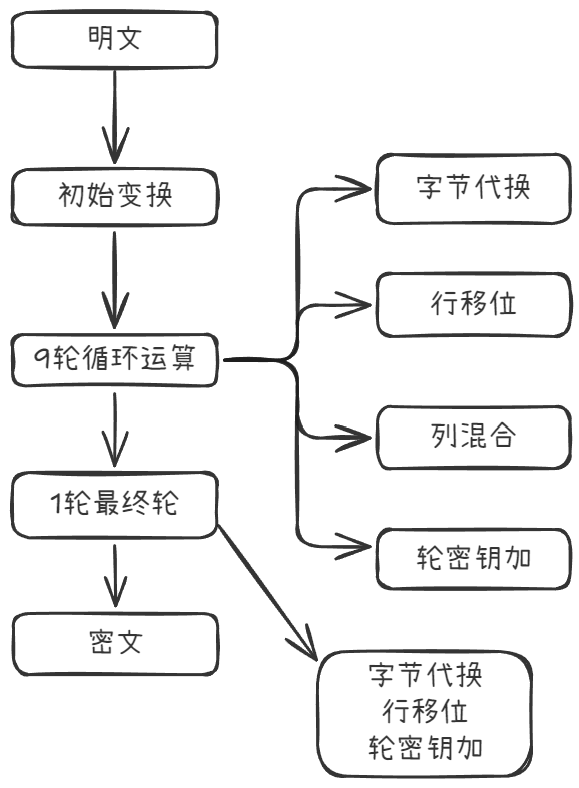
轮函数

• 字节代换
• 行移位
• 列混合（最后一轮没有）
• 轮密钥加

密钥编排

轮密钥比特数等于 $分组长度\times (轮数+1)$

• 128比特明文经10轮加密，总共需要$(10+1)×128=1408$ 比特的密钥

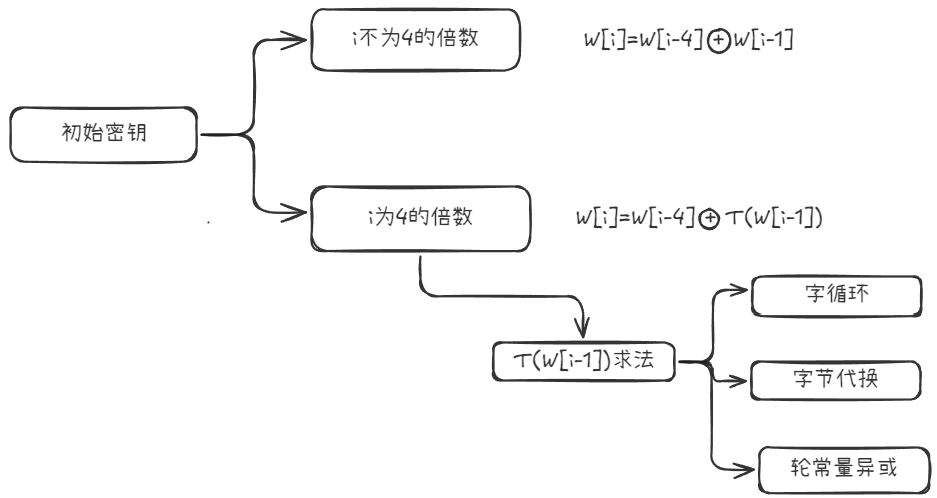
• 字节循环
• 字节代换
• 轮常量异或

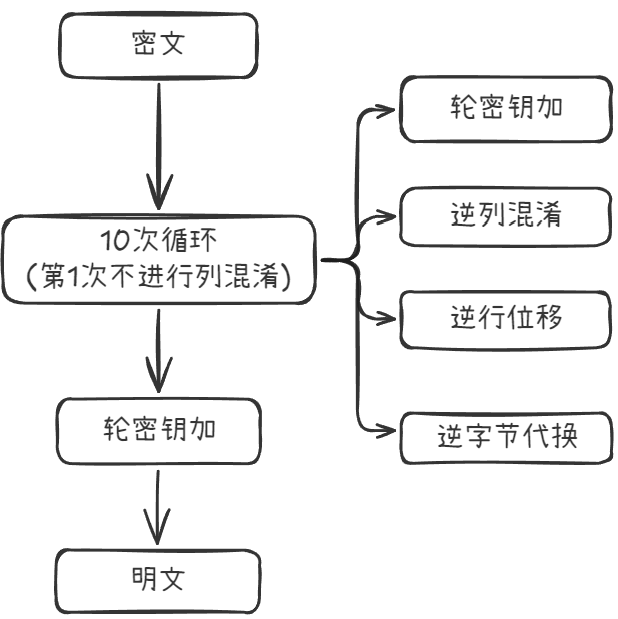
解密变换

• 执行顺序相反
• 字节代换表不一样
• 行位移由向左移动变为向右移动
• 列混淆的左乘数组不一样

列混合计算

• $f(a)$，若$a\leq 0x80$ 返回$2*a$
  否则返回$((2*a) \mod 0x100) \oplus 0x1B$
• 若乘法操作中一个数值是$2^n$，则可用以下公式
  $0x01\otimes a=a$
  $0x02\otimes a=f(a)$
  $0x04\otimes a=f(0x02\otimes a)$
  $0x08\otimes a=f(0x04\otimes a)$
  $0x10\otimes a=f(0x08\otimes a)$
• 非$2^n$可以拆分后相加（异或）

其他分组密码

1. “下列哪个是我国的商用分组密码标准？” 答案：SM4
2. “以混合使用不同代数群（模加、模乘、异或）的运算为主要设计特点的分组密码算法是？” 答案：IDEA
3. “请简述分组密码的两种主要迭代结构，并各举一例说明”
   答案：Feistel结构，例如DES和SM4；SPN结构，例如AES

分组密码运行模式

工作模式	填充	解密调用解密算法模块	能否并行计算	错误传播特性	主要应用场景
ECB (电子密码本)	Y	Y	加密和解密均可并行。	无错误传播	加密短的 、随机性强的数据（如密钥）。
CBC (密码分组链接)	Y	Y	加密不可并行；解密可并行。	影响2个	通用的大块 数据加密、认证。
CFB (密文反馈)	N	N	加密不可并行；解密可并行。	影响多个	通用的大块数据加密、认证。
OFB (输出反馈)	N	N	加密和解密均不可并行。	无错误传播	易出错的信道。
CTR (计数器模式)	N	N	加密和解密均可并行。	无错误传播	需要高速、并行处理的场合。

CFB模式
加密过程中，$P_1$误传，将影响$C_1 - C_9$
解密过程中$C_1$出错，会影响$P_1-P_9$

---

五、流密码

流密码核心：伪随机数发生器PRG

同步流密码

密钥流的生成独立于明文，仅与密钥和内部状态有关 。

• 优点：没有错误传播，密文中一个bit错误只影响解密后对应的一个bit
• 缺点：要求收发双方严格同步，否则解密失败
• 例子：OFB、CTR

自同步流密码

密钥流的生成与最近接收的若干个密文字符有关

• 优点：具有自同步能力。如果传输中出现错误或数据丢失，只会在接下来的几个字符内产生错误，之后系统能自动恢复同步
• 缺点：评估安全性困难，存在有限错误传播
• 例子：CFB

线性反馈移位寄存器LFSR

结构：由一个n级的移位寄存器和一个反馈函数组成

• 每次时钟脉冲（进动一拍），寄存器中的所有位向右移一位，最右边的一位作为输出
• 最左边一位由反馈函数的值来填充。反馈函数是寄存器中某些位（称为抽头 (tap)）的线性组合（异或运算）

n级LFSR输出的序列的周期 r 不依赖于寄存器的初始值，依赖于反馈函数，或者说特征多项式 p(x)

特征多项式

$p(x)=1+c_1x+c_2x^2+...+c_nx^n$

m序列 （最大长度序列）

• 一个n级LFSR能够产生的序列，其周期的最大值是$2^n-1$
• 能够达到最大周期的序列称为m序列
• 一个LFSR能生成m序列的充要条件是，它的特征多项式是GF(2)上的一个n次本原多项式

已知明文攻击

1. 截获一段明文和对应的密文，异或得到密钥流
2. LFSR级数$n$，只需要知道$2n$位密钥流输出
3. 解方程确定反馈函数（特征多项式）

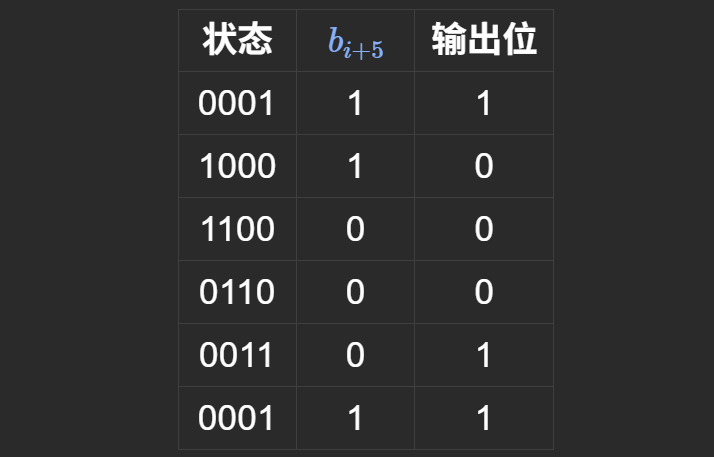
反馈函数：$b_{i+5}=b_{i+4}\oplus b_{i+3}\oplus b_{i+2}\oplus b_{i+1}(i\geq 0)$
初始状态为 0001：

周期为5，输出序列10001

提升LFSR安全性的方法：引入非线性

非线性组合生成器：Geffe生成器
非线性滤波生成器
钟控生成器

RC4

• 使用一个256字节大小的非线性数据表（S表）
• 两个计数器 I 和 J ，初值都为0

填空

• 流密码的设计思想来源于理论上绝对安全的一次一密 密码体制
• 流密码使用一个短的种子密钥，通过一个伪随机数生成器（PRG） 来产生一个长的、看似随机的密钥流
• 流密码的安全性完全取决于其密钥流 的随机性 和不可预测性
• 同步流密码 的密钥流生成独立于明文和密文，收发双方必须保持严格同步
• 自同步流密码 的密钥流生成与最近接收的若干个密文位有关，具有自动恢复同步的能力
• 分组密码的OFB和CTR模式可以看作是同步流密码，而CFB模式是自同步流密码
• 当n级LFSR的特征多项式为本原多项式 时，其输出序列的周期可以达到最大值 $2^n−1$，这种序列称为m序列
• 一旦反馈函数 被确定，整个密钥流序列都可以被预测，因此密码系统被完全破解
• RC4 不使用LFSR，而是维护256字节的S盒
• 流密码的致命弱点是绝不能重复使用同一个密钥流（密钥/IV对），否则攻击者可以通过异或两个密文得到两个明文的异或值，从而破解明文
• 软件算法：Rabbit、Salsa20；硬件算法：Grain-128、Trivium

---

六、Hash函数和MAC

Hash函数

定义与目标

将任意长度的消息 $x$ 压缩为固定长度的值 $y$
应用：检测消息完整性，提高数字签名速度

基本属性

• 压缩性
• 有效性
• 安全属性

三大安全属性

• 抗原像（单向性）：已知一个哈希值$h$，找到$M$使得$H(M)=h$在计算上不可行
• 抗第二原像：对于给定的消息$M_1$，要发现另一个消息$M_2$， 满足$H(M_1)=H(M_2)$在计算上不可行
• 抗（强）碰撞：找任意一对不同的消息$M_1$、$M_2$，使$H(M_1)= H(M_2)$在计算上不可行
• 分析复杂度：抗原像$O(2^n)$、抗第二原像性$O(2^n)$、抗强碰撞$O(2^{n/2})$

生日攻击

设Hash函数$h$的输出值长$n$比特，则经过约 $2^{n/2}$ 次杂凑运算，找到一对碰撞 $(x, x')$ 的概率大于1/2
对安全性的影响

• 生日攻击主要威胁抗强碰撞性
• 将寻找一个$n$比特的Hash函数碰撞计算复杂度从$O(2^n)$降到$O(2^{n/2})$

常用构造与算法

Merkle-Damgård (MD) 迭代结构：MD5, SHA-1, SHA-2
海绵结构：SHA-3、SM3
著名算法

• MD5：输出128，不安全
• SHA-1：输出160，不安全
• SHA-2：包括SHA-256、SHA-512等，安全
• SM3（Keccak）：我国商用密码杂凑算法标准，输出256位

消息认证码 (MAC)

定义与目标

$MAC$是一种使用共享密钥 $k$ 和消息 $M$ 来生成一个固定长度标签 $t$ 的算法，即 $t=MAC_k​(M)$
目标：消息完整性、消息源认证

MAC与Hash函数的根本区别

• MAC：需要一个秘密密钥。只有知道密钥的通信双方才能计算和验证MAC值，因此它能提供认证性。
• Hash函数：是无密钥的。任何人都可以计算消息的哈希值，因此它本身只能保证完整性，不能提供认证。

构造

基于分组密码构造（CBC-MAC）
基于分组密码的CBC工作模式来构造 。将消息用CBC模式加密，取最后一个密文块作为MAC值
基于哈希函数构造（HMAC）
$MAC=H((K⊕opad)‖H(K⊕ipad‖text))$

填空

• 现代广泛使用的Hash函数（如MD5、SHA-1）大多采用MD迭代结构，它通过一个压缩函数来迭代处理消息分组
• 我国发布的商用密码标准 中的Hash函数是SM3算法
• 消息认证码 (MAC) 是一种利用共享密钥和消息来生成一个固定长度认证标签的技术
• MAC的主要目标是同时保证消息的完整性和消息来源的认证性
• MAC与Hash函数的根本区别在于：MAC的生成和验证需要一个收发双方共享的秘密密钥，而Hash函数是无密钥的
• 对MAC算法最强的安全要求是在选择消息攻击下达到存在性不可伪造，即攻击者无法在不知道密钥的情况下为任何新消息伪造出合法的MAC值

---

七、公钥加密体制

基本思想

解决的问题

密钥分发、不可抵赖性

公钥 vs 对称密码

优势：密钥简化；支持数字签名、身份认证；密钥管理方便
不足：计算开销大；密钥长度长；存在中间人攻击

公钥加密模型

• 密钥生成过程：接收消息的端系统产生一对密钥$(PK_A,SK_A)$，$PK_A$是公开钥（用于加密）， $SK_A$是秘密密钥（用于解密）
• 加密过程：Bob想向Alice发送消息$m$，则获取Alice的公开密钥$PK_A$，加密得密文$c = E_{PK_A}[m]$, 其中$E$是加密算法
• 解密过程：Alice收到密文$c$后，用自己的秘密钥$SK_A$解密，表示为$m = D_{SK_A}[c]$，其中$D$是解密算法

理论基础：单向陷门函数OTF

单向性：一个函数正向计算很容易，但反向计算（求逆）在计算上是不可行的
陷门：它是一种特殊的单向函数，如果你掌握了一个“秘密信息”（即陷门），那么求逆就变得非常容易了
在公钥密码中，公钥定义了单向函数，私钥就是那个“陷门”

基于背包的单向陷门函数

密钥生成

• 生成一个长度为$n$的超递增背包向量$B=(b_1,b_2,...,b_n)$，作为私钥
• 选择一个模数 $k$ 和一个乘数 $t$
• 计算得到公钥$A=(a_1,a_2,...,a_n)$ $a_i \equiv t \cdot b_i \pmod{k}, \quad \text{for } i=1, 2, \dots, n$

加密

• 明文串$M$
• 发送方使用接收方的公钥 $A$。他将明文中为“1”的位所对应的公钥向量中的元素相加，得到的总和就是密文 $C$

解密

• 接收方收到密文 $C$，对 $C$ 进行变换 $S' \equiv C \cdot t^{-1} \pmod{k}$
• 求解超递增背包问题 $S' = \sum_{i=1}^{n} m_i \cdot b_i$

RSA公钥加密体制

安全性基础：基于大整数分解问题的困难性
密钥长度介于1024比特至2048比特之间的RSA是安全的
密钥生成算法：

• 选取两个非常大的素数 $p$ 和 $q$
• 计算模数 $n=p×q$
• 计算欧拉函数 $ϕ(n)=(p−1)(q−1)$
• 选取一个整数 $e$，使其满足 $1<e<ϕ(n)$ 且 $gcd(e,ϕ(n))=1$
• 计算 $d$，使其满足 $d⋅e≡1(modϕ(n))$
• 公钥为 $(e,n)$，私钥为 $(d,n)$

加解密算法：

• 加密：$c=m^e \pmod n$
• 解密：$m=c^d \pmod n$

安全参数要求：

• 选择足够大的长度相当的素数$p$，$q$，且$|p-q|$较大
• $(p-1)$和$(q-1)$存在大的素因子
• $\gcd(p-1,q-1)$较小
• e对所有用户可以是相同的，建议使用$e=2^{16}-1 = 65535$，不能太小
• 解密指数$d$比较大
• 不同用户不共用模数$n$

参数选择不当的攻击：

• 共模攻击：使用了相同的模数 $n$
  • 攻击者得到密文 $c_1\equiv m^{e_1}\pmod N$，$c_2\equiv m^{e_2}\pmod N$
  • $e_1$与$e_2$互素，根据扩展欧几里得算法，存在$re_1+se_2=1$
  • 攻击者计算$c_1^r\cdot c_2^s\pmod N$
  • $c_1^r \cdot c_2^s \equiv (m^{e_1})^r \cdot (m^{e_2})^s \equiv m^{re_1} \cdot m^{se_2} \equiv m^{re_1 + se_2}\equiv m \pmod{N}$
• 低加密指数攻击：使用小的$e$
  • 小的$e$可能导致$m^e<N$，模数不再起作用，密文的计算变为$c=m^d$
  • 攻击者直接计算$d=\sqrt[e]{c}$
• 低解密指数攻击：使用小的$d$
  • 数学原理：连分数（把一个数转换成一串分式）
  • 私钥满足$ed\equiv 1 \pmod {\phi(N)}$，即$ed=k\phi(N)+1$
  • 若$p,q$比较接近，则$\phi(N)$与$N$非常接近
  • 得到$ed\approx kN$，$\frac{e}{N}$的连分数展开中很有可能有$\frac{k}{d}$，由此恢复出$d$
• p和q差值小：$|p-q|$小
  • 费马分解法
  • $p$和$q$都接近$\sqrt{N}$，$(p+q)/2$也接近$\sqrt{N}$
  • 令$x=(p+q)/2$，$y=(p-q)/2$
  • $N=pq=(x+y)(x-y)=x^2-y^2$
  • 从$\lfloor N \rfloor$开始尝试$x$，检查$x^2-N$是否为完全平方数，从而分解$N$
• p-1或q-1包含小素因子
  • 重复加密攻击
  • 攻击者获取密文$c=m^e\pmod n$
  • 用公钥反复加密$c^e=(m^e)^e=m^{e^2}\pmod n$
    重复$t-1$次加密，得到$c^{e^{t-1}} = m^{e^t} \pmod n$
  • 当攻击者发现某一次加密变回密文$c$
    即$c^{e^{t}} =m^{e^{t+1}}=c \pmod n$，则$t-1$次的结果就是明文$m$

中间人攻击过程

• Mallory截获Alice发往Bob的 $Y_A$
• Mallory自己生成一个私钥 $m$，计算 $Y_M​=g^m \pmod p$。他将自己的 $Y_M$​ 发送给Bob，冒充是Alice发送的​
• Mallory同时将自己的 $Y_M$​ 发送给Alice，冒充是Bob发送的
• Alice计算出的共享密钥是 $K_{AM}​=(Y_M​)^a \pmod p$
• Bob计算出的共享密钥是 $K_{BM}​=(Y_M​)^b \pmod p$
• 此时，Mallory可以分别计算出他与Alice的密钥 $K_{AM}​=(Y_A​)^m \pmod p$ 和与Bob的密钥 $K_{BM}​=(Y_B​)^m \pmod p$

ElGamal单向陷门函数

安全性基础：基于离散对数问题的困难性
密钥生成（接收方完成）

• 选择一个大素数 $p$，生成元 $g$，选择私钥 $x$
• 计算$y=g^x \pmod p$
• 公钥 $(p,g,y)$

加密（发送方完成）

• 待发送明文 $M$
• 选择一个一次性整数 $k$
• 计算 $C_1=g^k \pmod p$
• 计算 $C_2=M \cdot y^k \pmod p$
• 密文 $(C_1,C_2)$

解密（接收方完成）

• $M=C_2​⋅(C_1^x​)^{−1} \pmod p$

椭圆曲线密码体制ECC

安全性基础：椭圆曲线上的离散对数问题 (ECDLP)，即已知点 $P$ 和点 $Q=kP$，在计算上难以求出整数 $k$
最大优势：密钥短，安全性高

填空

• 公钥密码学的理论基础是陷门单向函数
• 使用接收方的公钥加密、接收方的私钥解密，可以实现保密通信
• RSA算法的安全性建立在大整数因子分解问题的困难性之上
• Diffie-Hellman协议是一个密钥交换协议，它允许双方在公开信道上安全地协商出一个共享密钥，但它本身不提供身份认证，因此容易受到中间人攻击
• ECC的安全性建立在椭圆曲线上离散对数问题(ECDLP)的困难性之上
• ECC相对于RSA最主要的优势是：达到同等级别的安全强度时，可以使用更短的密钥
• 我国的SM2算法就是基于椭圆曲线的公钥密码标准

---

八、数字签名

基本概念

数字签名的作用

• 确认消息发送方的身份（来源认证）
• 确认消息内容的完整性
• 不可否认性（与MAC最根本的区别）

核心原理：“先哈希，再签名”
签名的三要素：密钥生成、签名、验证

• 密钥生成：用户生成一对公钥和私钥。公钥公开，私钥保密
• 签名过程：用自己的私钥 对消息的哈希值 进行签名
• 验证过程：用发送方的公钥 解开签名，得到一个哈希值 $(H_1)$
  • 自己独立计算收到的原始消息的哈希值 $(H_2)$。如果 $H_1 = H_2$，则签名有效

主流数字签名方案

基于RSA的签名方案

安全性基础：大整数分解难题

• 密钥生成：选两个大素数 $p$ 和 $q$，$n=pq$，$\phi(n)=(p-1)(q-1)$，$(e,\phi(n))=1$，计算 $d$ 满足$ed=1 \pmod {\phi(n)}$。
  $(n,e)$为验证密钥，$(n,d)$为签名密钥。
• 签名：$s=h(m)^d \pmod n$
• 验证：验证 $h(m)≡s^e \pmod n$

正确性证明

$s^e \equiv (h(m)^d)^e \pmod{n}\equiv h(m)^{de} \pmod{n}$
已知$de \equiv 1 \pmod{\phi(n)}$，即存在 $k$ 使$de = k \cdot \phi(n) + 1$代入上式：
$\equiv h(m)^{k \cdot \phi(n) + 1} \pmod{n}\equiv (h(m)^{\phi(n)})^k \cdot h(m)^1 \pmod{n}$
根据欧拉定理，$h(m)^{ϕ(n)}≡1 \pmod n$
$\equiv 1^k \cdot h(m) \pmod{n}\equiv h(m) \pmod{n}$

安全性要求

如果不用哈希，存在两种攻击

• 唯密钥攻击的存在性伪造
  • 选一个$s$作为签名，构造$m=s^e \pmod n$，发布签名$(m,s)$
  • 验证：显然成立
• 已知消息攻击的存在性伪造
  • 截获两个信息$m_1,m_2$，以及签名$s_1=m_1^d \pmod n$，$s_2=m_2^d \pmod n$
  • 构造新消息$m=m_1 \cdot m_2 \pmod n$和签名$s=s_1 \cdot s_2 \pmod n$
  • 验证：$s^e \equiv s_1^e \cdot s_2^e\equiv (m_1^d)^e \cdot (m_2^d)^e\equiv m_1 \cdot m_2 \equiv m \pmod n$

用哈希，攻击失效

• 第一种攻击：算出$m$后无法找到$H(m')=m$
• 第二种攻击：$H(m_1,m_2)\neq H(m_1)\cdot H(m_2)$

基于离散对数的数字签名

ElGamal签名

• 密钥生成：选一个素数$p$，生成元 $g$ 和随机数 $x$，计算$y=g^x \pmod p$
  公钥为$y$，$p$，$g$，私钥为$x$
• 签名
  • 选一个随机数 $k$，$k$ 与 $p-1$ 互质
  • 计算$r$：$r \equiv g^k \pmod{p}$
  • 计算$s$：$s \equiv (h(m) - xr)k^{-1} \pmod{p-1}$
• 验证：$y^r r^s \equiv g^{h(m)} \pmod{p}$

正确性证明

$s≡(h(m)−xr)k^{−1} \pmod {p−1}$
$ks≡h(m)−xr \pmod {p−1}$
即$ks=h(m)−xr+i(p−1)$，将其作为生成元 $g$ 的指数，由于$g^{p-1}\equiv 1 \pmod p$，
$g^{ks}\equiv g^{h(m)-xr}\equiv g^{h(m)}\cdot g^{-xr} \pmod p$
$g^{ks}\cdot g^{xr}\equiv g^{h(m)} \pmod p$
已知 $r\equiv g^k \pmod p$，$y=g^x \pmod p$，代入：
$r^s\cdot y^r\equiv g^{h(m)}\pmod p$

安全性要求

如果没有Hash，可以构造两种攻击

• 存在性伪造攻击
  • 攻击者选择一个数字 $e$
  • 制作签名 $(r,s)$，$r=g^ey \pmod p$，$s=-r \pmod {p-1}$
  • 制作消息 $m=es \pmod {p-1}$
  • 验证：$r^s\cdot y^r\equiv r^s\cdot g^{xr}\equiv g^{es}\cdot y^s \cdot y^r\equiv g^{-er}\equiv g^m \pmod p$
• 利用已知关系进行伪造

K值的安全性

• K泄露可求出密钥 $x$
  • 攻击者已知 $m$，可求出 $h(m)$，又已知签名 $(r,s)$ 和随机数 $k$
  • $s\equiv (h(m)-xr)k^{-1} \pmod {p-1}$
  • 求出 $x$：$x\equiv (h(m)-sk)r^{-1} \pmod {p-1}$
• 选择一样的 $k$，能求出密钥 $x$
  • 攻击者截获了两个不同消息 $m_1$、$m_2$ 和它们各自的签名 $(r, s_1)$、$(r, s_2)$。因为两次签名的 $r$ 值相同，攻击者便知晓 $k$ 被重用（$r$ 只依赖于 $k$）。于是攻击者计算出 $h(m_1)$ 和 $h(m_2)$
  • 将 $s_1$ 和 $s_2$ 的方程变形
    $s_1k\equiv (h(m_1)-xr) \pmod {p-1}$
    $s_2k\equiv (h(m_2)-xr) \pmod {p-1}$
  • 两式相减：$(s_1-s_2)k\equiv (h(m_1)-h(m_2)) \pmod {p-1}$
  • $k\equiv (h(m_1)-h(m_2))(s_1-s_2)^{-1} \pmod {p-1}$
  • 将 $k$ 带入原式求出私钥 $x$：$x\equiv (h(m_1)-s_1k)r^{-1} \pmod {p-1}$

Schnorr签名

ElGamal的变种，签名更短，计算更快
系统设置

• 素数 $p$ 和 $q$：$p$ 是一个大素数，$q$ 是 $p-1$ 的一个素数因子
• $g$: $g$ 是一个 $q$ 阶元，意味着 $g^q≡1 \pmod p$
• $h$: 一个安全的哈希函数，比如SHA-256

密钥生成

• 签名者选择一个随机数 $x$（1到q-1），作为私钥
• 计算公钥 $y=g^x \pmod p$
• 公钥 $(p,q,g,y)$

签名

• 选择随机数 $k$（1到q-1）
• 计算挑战 $c = h(m ||g^k)$
• 计算应答 $s = k + xc \pmod q$
• 签名为 $(c,s)$

验证

• 收到消息 $m$，和签名 $(c,s)$
• 验证 $h(m || g^s y^{-c}) = c$

参数长度

• 一般 $p$ 长度为1024bit, $q$ 为160-bit
• 签名$(c,s)$长度320bit

正确性证明

$g^sy^{-c}= g^{(k+xc)} y^{-c}= g^k g^{xc} y^{-c}= g^k g^{xc} (g^x)^{-c}= g^k g^{xc} g^{-xc}=g^k$
$h(m || g^s y^{-c})= h(m ||g^k)=c$

安全性要求

安全性依赖 $k$

DSA签名

密钥生成

• 素数 $p$ 和 $q$：$p$ 是一个大素数，$q$ 是 $p-1$ 的一个素数因子
• $g$: $g$ 是一个 $q$ 阶元，意味着 $g^q≡1 \pmod p$
• 选一个随机数 $x$（$1<x<q$）作为私钥
• 公钥：计算 $y=g^x \pmod p$

签名过程

• 选择随机数 $k$（$1<k<q$）
• $r = (g^k \pmod p) \pmod q$，如果计算出 $r=0$，必须重新选择一个 $k$
• $s = k^{-1}(h(m) + xr) \pmod q$，如果计算出 $s=0$，必须重新选择一个 $k$
• 签名为 $(r,s)$

验证过程

• 验证者收到消息 $M$ 和签名 $(r, s)$
• $u_1​=h(m)⋅s^{-1} \pmod q$
• $u_2​=r⋅s^{-1} \pmod q$
• $v=(g^{u_1}y^{u_2}\pmod p)\pmod q$
• 验证$v=r$

正确性证明

$v = ((g^{h(m) \cdot s^{-1}} (g^x)^{r \cdot s^{-1}}) \pmod p) \pmod q$
$v = ((g^{h(m) \cdot s^{-1} + xr \cdot s^{-1}}) \pmod p) \pmod q$
$v = (g^{(h(m) + xr)s^{-1}} \pmod p) \pmod q$
由$s = k^{-1}(h(m) + xr) \pmod q$解得$k \equiv (h(m) + xr)s^{-1} \pmod q$
因此得到：$v = (g^k \pmod p) \pmod q$
而$r = (g^k \pmod p) \pmod q$，因此$v=r$

安全性要求

重用 $k$：

• $s = k^{-1}(h(m) + xr) \pmod q$公式变形得到
  $s_1k\equiv (h(m_1)+xr) \pmod q$
  $s_2k\equiv (h(m_2)+xr) \pmod q$
• 相减得：$(s_1-s_2)k\equiv (h(m_1)-h(m_2))\pmod q$
  $k\equiv (h(m_1)-h(m_2))(s_1-s_2)^{-1} \pmod q$
• 带入 $k$ 解出私钥 $x$：$x\equiv (s_1k-h(m_1))r^{-1} \pmod q$

椭圆曲线数字签名（ECDSA）

• 基于“椭圆曲线上的离散对数问题”(ECDLP)
• 将数字签名算法（DSA） 的数学运算从传统的有限域 乘法群，平移到椭圆曲线 上的点群中去实现
• 在提供同等级别的安全强度下，ECC可以使用更短的密钥和签名
  • 计算速度更快
  • 存储空间占用更小
  • 网络传输带宽要求更低

特殊数字签名方案

盲签名

核心功能：签名者在不知道消息内容 的情况下对消息进行签名

• 不可追踪
  应用场景：需要保护用户隐私的场合，如电子投票、电子现金

群签名

核心功能：有管理员 的匿名，可追溯，平衡匿名 和问责
应用场景：需要以组织名义进行授权，但又不暴露具体执行人的场合，如公司部门的审批

环签名

核心功能：无管理员 的绝对匿名
应用场合：需要实现高强度的、不可追溯的匿名声明 的场合，如内部举报

门限签名

群组中超过一定数量（门限值） 的成员合作 才可以产生合法签名

多重签名

将多个人的数字签名汇总成一个签名数据进行传送

代理签名

原始签名者可以将自己的签名权在受控的条件下，安全地授权 给另一方，由代理者代为行使签名权

Fail-Stop数字签名方案

签名者可以出示伪造证明，证明这个签名确实不是他生成的，从而使伪造的签名失效

不可否认签名

没有签名者合作，接收者无法验证签名合法性

加密认证方式

同时实现保密性和认证性
外部保密方式（推荐）：先签名后加密，便于解决争议
内部保密方式：先加密后签名

填空与简答

数字签名 vs. 消息认证码 (MAC)

• 不可否认性是数字签名相对于MAC的根本区别，这个根本区别源于它们所使用的密钥类型不同
• MAC使用的是对称密钥，通信双方共享同一个密钥，任何一方都可以生成或验证MAC，这就导致无法向第三方证明某个MAC到底是谁生成的，所以不具备不可否认性
• 数字签名使用的是非对称密钥。签名必须用私钥，而私钥只有签名者自己持有。验证则使用公开的公钥。这种密钥的独占性，为不可否认性 提供了基础

一句话知识点

• 数字签名的主要作用是提供消息来源认证、消息完整性和不可否认性
• 现代数字签名的核心原理是“先哈希，再签名”
• 一个完整的数字签名方案由密钥生成、签名和验证三个算法组成
• 签名过程使用发送方的私钥，而验证过程使用发送方的公钥，因此任何人都可以进行验证
• ECDSA (椭圆曲线数字签名算法)是将DSA的运算逻辑平移到椭圆曲线群上实现的，其主要优势是在同等安全强度下，密钥和签名长度都更短

---

九、密钥管理

密钥管理的基本原则与层次结构

• 柯克霍夫原则：一个密码系统的安全性应该完全依赖于密钥的保密性，而不是算法的保密性
• 密钥生命周期：密钥从生成、建立、存储、使用、备份/恢复、更新、撤销 到最终销毁 的全过程，都需要进行安全管理
  • 密钥生成是密钥生命周期的基础 阶段
  • 密钥建立是密钥安全（完整、保密）到达密钥使用的各实体对象，分为密钥分配 和密钥协商
  • 密钥存储：基于口令的软保护、基于硬件的物理保护
• 密钥分级原则
  • 主密钥：最高层级的，通常由人工或物理方式保护，用来加密下层密钥
  • 密钥加密密钥：二级密钥，用来加密和解密会话密钥，不直接加密数据
  • 会话密钥：数据加密密钥，最低层级的，用于直接加密和解密数据，生命周期短
  • 相同点：目的都是为了保护数据安全，都用于加密操作
  • 不同点：安全级别不同、使用频率不同、生命周期不同等

密钥建立

密钥分配

核心：由一方（通信方或可信的第三方）生成密钥，然后安全地分发 给另一方

无密钥分配

流程

• A要发密钥$K$
• A选取素数$P$，随机数$a$，发送$(K^a,P)$
• B选随机数$b$，计算$K^{ab}$发给A
• A计算$K^{aba^{-1}}$得到$K^b$，发给B
• B解密得到$K_b$

基于对称技术的密钥分配

依赖于通信方之间已经存在的共享密钥，即密钥加密密钥 (KEK)

无中心的密钥分配

• A和B之间有共享的密钥加密密钥 $K_{AB}$
• 流程：A生成一个会话密钥$K_S$，用$K_{AB}$加密之后发给B

改进版：引入随机数 $N_1$​ 的目的是防止重放攻击，确保B收到的不是过期的、被攻击者截获重发的旧请求

• A请求会话密钥，发送随机数$N_1$
• B收到$N_1$，选择会话密钥$K_S$，用共享密钥$K_{AB}$加密$K_S||N_1$发送
• A解密得到 $K_S$，用$K_S$加密$f(N_1)$，告诉B已收到

$N$个用户，需要维护 $N(N−1)/2$ 个KEK

有中心的密钥分配（KDC模式）

核心思想：引入一个所有用户都信任的密钥分发中心 (KDC)，用户跟KDC共享主密钥
存在问题：用户多、分布广→解决：分层KDC

流程

• A向KDC发出和B会话的请求
• KDC生成一个全新的会话密钥$K_S​$
• KDC将 $K_S$​ 分别用 $K_{AT}​$ 和 $K_{BT}$​ 加密
• A和B各自解密得到会话密钥 $K_S$

$N$个用户只需要$N$个主密钥

Needham-Schroeder密钥分发协议

• 密钥分发技术的里程碑
• 在KDC模式下，引入随机数N

流程

• A向KDC发出会话密钥请求：$Request||N_1$
• KDC发出应答：$E_{K_{AT}}(K_S||N_1||E_{K_{BT}}(K_S||ID_A||N_1))$
• A解密得到$K_S$，转发$E_{K_{BT}}(K_S||ID_A||N_1)$
• B解密得到$K_S$，用$K_S$加密随机数$N_2$发给A
• A收到回复$K_S$加密的$N_2-1$

安全缺陷

• 旧的会话密钥$K_S$泄露，攻击者可以重放截获的$E_{K_{BT}}(K_S||ID_A||N_1)$冒充A与B连接
• A不能确认B是否拿到$K_S$，攻击者可以伪造$N_2$

Kerberos密钥分发协议

引入时间戳$T_{KDC}$和生存时间$L$
流程

• 与NS分发类似，增加：
• KDC应答A：$E_{K_{AT}}(K_s \Vert T_{KDC} \Vert L \Vert ID_B \Vert E_{K_{BT}}(K_s \Vert ID_A \Vert T_{KDC} \Vert L))$
• A判断$L$与$T_{KDC}$是否正确，用$K_S$加密时间戳发给B
• B拿$K_S$解密得$T_{KDC}$和$L$，验证，应答$T_A+1$

基于公钥技术的密钥分配

核心思想：利用非对称加密 的特性，过程非常简洁
流程

• A把身份$ID_A$和公钥$PK_A$发给B
• B用公钥$PK_A$加密$K_S$、身份$ID_B$发给A
• A用私钥解密得到$K_S$

安全问题

• 安全性完全依赖于公钥的真实性
• B拿到的是攻击者伪造的$PK_A$则密钥泄露
• 依赖于PKI 和数字证书 来保证公钥真实性

密钥协商

核心：允许通信双方在不安全的公开信道上，通过交换信息来共同计算 出一个共享的秘密密钥
与密钥分配的区别：任何一方都不能单方面决定最终的密钥值

Diffie-Hellman (D-H) 密钥交换协议

流程

• 双方公开约定大素数 $p$ 和生成元 $g$
• A选择随机数 $a$，将公钥 $A=g^a \pmod p$发给B
• B选择随机数 $b$，将公钥 $B=g^b \pmod p$发给A
• A计算共享密钥 $K=B^a=(g^b)^a=g^{ab} \pmod p$
• B计算共享密钥 $K=A^b=(g^a)^b=g^{ab} \pmod p$

中间人攻击

• 原因：D-H协议不包含对通信双方的身份认证
• 攻击流程
  • 攻击者M截获A发给B的$K_A$​，生成随机数 $m$，将$K_M​=g^m \pmod p$冒充A的公钥发给B
  • 攻击者M截获B发给A的$K_B$​，将$K_M​$冒充B的公钥发给A
  • A与M协商出密钥 $K_{AM}$​，B与M协商出密钥 $K_{BM}$​，截获两边的通信

站-站协议（STS协议）

改进版Diffie-Hellman协议：增加了使用数字签名 进行双向身份认证
流程

• A生成公钥$A$发给B
• B生成公钥$B$，用私钥对双方公钥$A,B$进行签名，用共享密钥$K$对签名加密$E_B=E_K[Sig_B(A,B)]$，将公钥$B$、加密后签名$E_B$发给A
• A计算$K$，用$K$解密得$E_B$，用公钥$B$验签。
• A用私钥对双方公钥签名，用$K$对签名加密发给B
• B解密并用公钥$A$验签

NS密钥协商协议

Needham-Schroeder密钥分发协议的公钥版本
流程

• 与NS密钥分发类似，区别：
  • KDC不生成会话密钥，只用私钥对A和B的公钥签名（公证人）
  • 双方拿到可信公钥还要交换随机数，双方用$N_A$和$N_B$算出会话密钥

安全性：仍然存在中间人攻击

公钥基础设施PKI

用于生成、管理、存储、分发和撤销数字证书 的体系
核心目的：解决公钥的分发和信任 问题
核心技术：数字证书——由可信的第三方证书颁发机构 (CA) 签发的一种电子凭证

PKI主要组成

• CA证书颁发机构
• RA注册机构
• CRL证书撤销列表
• 时间戳服务
• TSA时间戳权威

证书管理

• 证书的注册与发布：用户向RA提交申请，RA审核身份后，由CA生成并签发证书，最后将证书发布到公共目录（证书库）中供人查询
• 证书验证：
  • 检查证书是否在证书撤销列表 (CRL) 中
  • 检查证书的有效期
  • 检查证书的预期用途是否与当前操作相符
  • 使用CA的公钥验证证书自身的签名是否有效
• 证书撤销：CA发布CRL公示

秘密共享

• 参数选择：选成员个数 $n$ 和门限值 $t$
• 秘密分割：将秘密 $S$ 分为 $n$ 个子共享$S_1,S_2,…,S_n$，秘密分配给 $n$ 个成员
• 秘密恢复：输入至少 $t$ 个子共享，输出秘密 $S$

Shamir门限方案

核心思想：平面上 t 个点可以唯一确定一个 t−1 次多项式
秘密分割阶段

• 将秘密 $S$ 作为多项式 $f(x)$ 的常数项（$f(0)=S$）。
• 构造一个随机的 $t−1$ 次多项式：$f(x)=S+a_1​x+a_2​x^2+⋯+a_{t−1}​x^{t−1}$
• 在这个多项式曲线上取 $n$ 个不同的点 $(x_1​,y_1​),(x_2​,y_2​),…,(x_n​,y_n​)$，将每一个点作为一份“秘密份额”分发给 $n$ 个参与者

秘密恢复阶段

• 任何 t 个或更多 的参与者凑齐他们的份额（即 $t$ 个点），就可以利用拉格朗日插值法 唯一地恢复出原始的 $t−1$ 次多项式 $f(x)$
• 多项式被恢复，令 $x=0$ 即可求得常数项，即秘密 $S$

填空

• 为了在安全和效率间取得平衡，密钥通常采用分级管理，用高层级、长生命周期的密钥保护低层级、短生命周期的密钥
• 经典的三层密钥结构从上到下依次是：主密钥、密钥加密密钥(KEK) 和会话密钥
• Diffie-Hellman协议是密钥协商的典型代表，其安全性建立在离散对数难题之上
• 经典的D-H协议因缺乏身份认证机制，容易受到中间人攻击
• 站-到-站(STS)协议通过引入数字签名和证书来为D-H交换增加双向身份认证，从而有效抵御中间人攻击
• 注册机构(RA)在CA颁发证书前，负责审核和验证申请者的真实身份
• CA通过使用自己的私钥对证书内容进行数字签名，来保证证书的真实性和不可篡改性
• 密钥托管是一种允许被授权的第三方（如政府机构）在特定法律条件下恢复用户密钥的机制